Leibniz is a python package which provide facilities to express learnable differential equations with PyTorch
We also provide UNet, ResUNet and their variations, especially the Hyperbolic blocks for ResUNet.
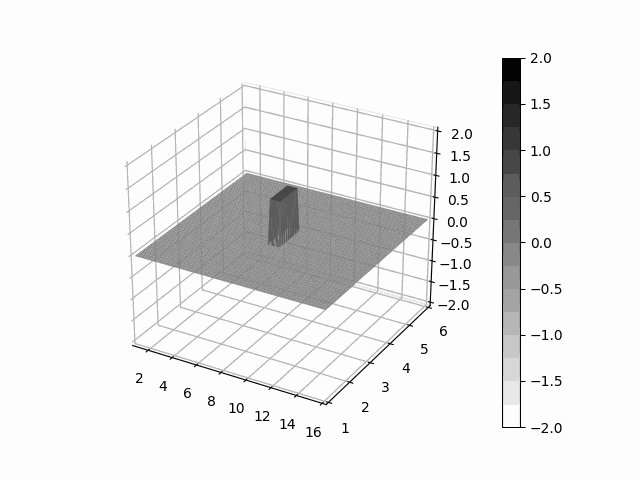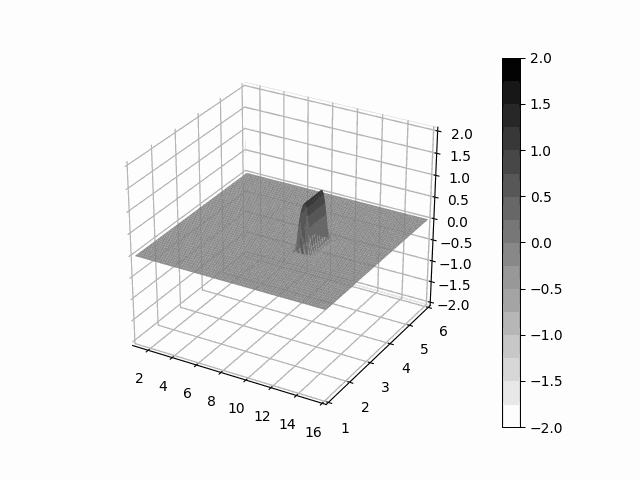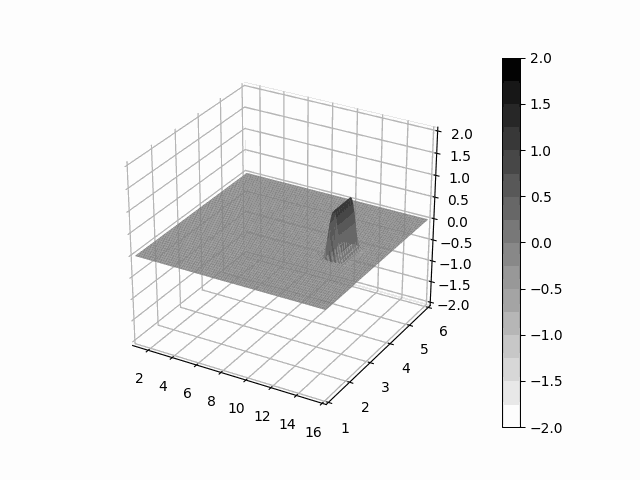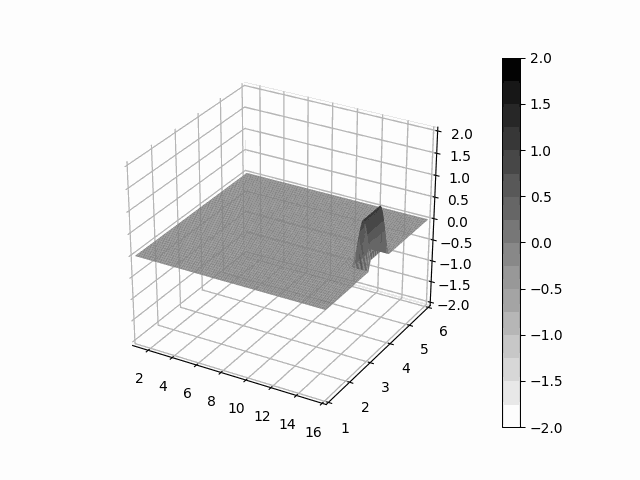
pip install leibnizAs an example we solve a very simple advection problem, a box-shaped material transported by a constant steady wind.
import torch as th
import leibniz as lbnz
from leibniz.core3d.gridsys.regular3 import RegularGrid
from leibniz.diffeq import odeint as odeint
def binary(tensor):
return th.where(tensor > lbnz.zero, lbnz.one, lbnz.zero)
# setup grid system
lbnz.bind(RegularGrid(
basis='x,y,z',
W=51, L=151, H=51,
east=16.0, west=1.0,
north=6.0, south=1.0,
upper=6.0, lower=1.0
))
lbnz.use('x,y,z') # use xyz coordinate
# giving a material field as a box
fld = binary((lbnz.x - 8) * (9 - lbnz.x)) * \
binary((lbnz.y - 3) * (4 - lbnz.y)) * \
binary((lbnz.z - 3) * (4 - lbnz.z))
# construct a constant steady wind
wind = lbnz.one, lbnz.zero, lbnz.zero
# transport value by wind
def derivitive(t, clouds):
return - lbnz.upwind(wind, clouds)
# integrate the system with rk4
pred = odeint(derivitive, fld, th.arange(0, 7, 1 / 100), method='rk4')from leibniz.unet import UNet
from leibniz.nn.layer.hyperbolic import HyperBottleneck
from leibniz.nn.activation import CappingRelu
unet = UNet(6, 1, normalizor='batch', spatial=(32, 64), layers=5, ratio=-1,
vblks=[4, 4, 4, 4, 4], hblks=[1, 1, 1, 1, 1],
scales=[-1, -1, -1, -1, -1], factors=[1, 1, 1, 1, 1],
block=HyperBottleneck, relu=CappingRelu(), final_normalized=False)We provide a ResUNet implementation, which is a UNet variation can insert ResNet blocks between layers. The supported ResNet blocks are include
- Pure ResNet: Basic, Bottleneck block
- SENet variations: Basic, Bottleneck block
- Hyperbolic variations: Basic, Bottleneck block
We support 1d, 2d, 3d UNet.
normalizor are include:
- batch: BatchNorm
- layer: LayerNorm
- instance: InstanceNorm
Other hyperparameters are include:
- spatial: the sizes of the spatial dimentions
- ratio: the ratio to decide the intial number of channels into the UNet
- vblks: how many vertical blocks is inserted between two layers
- hblks: how many horizontal blocks is inserted in the skip connections
- scales: scale factors(power-2-based) on the spatial dimentions
- factors: expand or shrink factors(power-2-based) on the channels
- final_normalized: wheather to scale to final result between 0 to 1
Piecewise Linear normalizor provide an learnable monotonic peicewise linear functions and its inverse fucntion. The API is shown as below
from leibniz.nn.normalizor import PWLNormalizor
# on 3 channels, given 128 segmented pieces, and assuming the input data have a zero mean and 1.0 std
pwln = PWLNormalizor(3, 128, mean=0.0, std=1.0)
normed = pwln(input)
output = pwln.inverse(normed)python3 setup.py sdist bdist_wheel
python3 -m twine upload dist/*
git tag va.b.c master
git push origin va.b.cWe included source code with minor changes from torchdiffeq by Ricky Chen, because of two purpose:
- package torchdiffeq is not indexed by pypi
- package torchdiffeq is very convenient and mandatory
All our contribution is based on Ricky's Neural ODE paper (NIPS 2018) and his package.